zoey
点击国内主页可以让浏览速度加快哦 ~ ！
LINKS:
friend(ironic333)主页国内主页

关于HDOJ 1330题(Deck) 的理解(C/C++)

2019-08-20 hdoj cout输出格式 物理 重心 杠杆原理 力矩计算 South Central USA 1998
Word count: 2.5k | Reading time: 11min


    题目首先从编程算法出发的话其实是道简单题（甚至说水题），就是其中关于卡牌重心位置的计算用到了一些遗忘了的物理知识。鉴于大二原专业学过理论力学的自己感觉有必要记录一下（表示真的不会算力学题了些微伤心。


    此外，这题还设计了输出格式的要求：

  1. 输出字符的长度要求
  2. 对齐要求（不过实际代码默认地就是靠对齐了）
  3. 小数点后精确数位要求


Deck(桌檐叠卡牌)

Deck
Time Limit: 2000/1000 MS (Java/Others)
Memory Limit: 65536/32768 K (Java/Others)

Problem Description
    A single playing card can be placed on a table, carefully, so that the short edges of the card are parallel to the table’s edge, and half the length of the card hangs over the edge of the table. If the card hung any further out, with its center of gravity off the table, it would fall off the table and flutter to the floor. The same reasoning applies if the card were placed on another card, rather than on a table.

Two playing cards can be arranged, carefully, with short edges parallel to table edges, to extend 3/4 of a card length beyond the edge of the table. The top card hangs half a card length past the edge of the bottom card. The bottom card hangs with only 1/4 of its length past the table’s edge. The center of gravity of the two cards combined lies just over the edge of the table.

Three playing cards can be arranged, with short edges parallel to table edges, and each card touching at most one other card, to extend 11/12 of a card length beyond the edge of the table. The top two cards extend 3/4 of a card length beyond the edge of the bottom card, and the bottom card extends only 1/6 over the table’s edge; the center of gravity of the three cards lines over the edges of the table.

If you keep stacking cards so that the edges are aligned and every card has at most one card above it and one below it, how far out can 4 cards extend over the table’s edge? Or 52 cards? Or 1000 cards? Or 99999?

Input
    Input contains several nonnegative integers, one to a line. No integer exceeds 99999.

Output
    The standard output will contain, on successful completion of the program, a heading: 

# Cards Overhang

(that’s two spaces between the words) and, following, a line for each input integer giving the length of the longest overhang achievable with the given number of cards, measured in cardlengths, and rounded to the nearest thousandth. The length must be expressed with at least one digit before the decimal point and exactly three digits after it. The number of cards is right-justified in column 5, and the decimal points for the lengths lie in column 12.

Sample Input

1
2
3
4
5
1 
2 
3 
4 
30

Sample Output
The line of digits is intended to guide you in proper output alignment, and is not part of the output that your solution should produce. 

1
2
3
4
5
6
7
12345678901234567
# Cards  Overhang
    1     0.500
    2     0.750
    3     0.917
    4     1.042
   30     1.997

Source

    South Central USA 1998



原题链接

More info:Question

cout输出控制（复习）

之前其它的hdoj题目中也有类似的输出格式要求题目，详见：

More info:hdoj1012


More info:hdoj1014

小数位数的控制

首先是头文件

1
#include <iomanip>

然后就是用法了

1
cout << fixed<< setprecision(n)<< 变量;

当然，通过这次的题目还发现了一写小细节问题，之前都没怎么注意的。原来cout输出时，默认地，会删除掉多余的小数点后的0。于是去搜了一下怎么让cout输出不去删掉小数点后多余的0：

1
cout.setf(ios_base::fixed,ios_base::floatfield);

然后以下是自己结合网上给的关于控制小数位数的一些测试代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<iostream>
#include <iomanip>
using namespace std;
int main()
{
    const double value = 12.3456789;
    cout << value << endl; // 默认以6精度，所以输出为 12.3457 
    cout << setprecision(4) << value << endl; // 改成4精度，所以输出为12.35 
    cout << setprecision(8) << value << endl; // 改成8精度，所以输出为12.345679 
    cout << fixed << setprecision(4) << value << endl; // 加了fixed意味着是固定点方式显示，所以这里的精度指的是小数位，输出为12.3457 
    cout << value << endl; // fixed和setprecision的作用还在，依然显示12.3457 
    cout.unsetf(ios::fixed); // 去掉了fixed，所以精度恢复成整个数值的有效位数，显示为12.35 
    cout << value << endl;
    cout.precision(6); // 恢复成原来的样子，输出为12.3457 
    cout << value << endl<<endl;

    //在C++中，cout语句会自动删除浮点数小数部分多余的0
    const double value2 = 12.0000000;
    cout << value2 << endl; // 默认以6精度，但是cout语句会自动删除浮点数小数部分多余的0，所以输出为12
    cout << setprecision(4) << value2 << endl; // 改成4精度，输出为12 
    cout << setprecision(8) << value2<< endl; // 改成8精度，输出为12 
    cout << fixed << setprecision(4) << value2 << endl; // 加了fixed意味着是固定点方式显示，所以这里的精度指的是小数位，输出为12.0000 
    cout << value2 << endl; // fixed和setprecision的作用还在，依然显示12.0000 
    cout.unsetf(ios::fixed); // 去掉了fixed，精度恢复成整个数值的有效位数，但是依旧自动删除多余0，显示为12 
    cout << value2 << endl;
    cout.precision(6); // 恢复成原来的样子，输出为12 
    cout << value2 << endl<<endl;
    
    //cout.setf(ios_base::fixed,ios_base::floatfield);可避免自动删除多余0的效果
    const double value3 = 12.0000000;
    cout.setf(ios_base::fixed, ios_base::floatfield);
    cout << value3 << endl; // 默认以6精度，所以输出为 12.000000 
    cout << setprecision(4) << value3 << endl; // 改成4精度，所以输出为12.0000 
    cout << setprecision(8) << value3 << endl; // 改成8精度，所以输出为12.00000000 
    cout << fixed << setprecision(4) << value3 << endl; // 加了fixed意味着是固定点方式显示，所以这里的精度指的是小数位，输出为12.0000 
    cout << value3 << endl; // fixed和setprecision的作用还在，依然显示12.0000 
    cout.unsetf(ios::fixed); // 去掉了fixed，所以精度恢复成整个数值的有效位数，显示为12 
    cout << value3 << endl;
    cout.precision(6); // 恢复成原来的样子，输出为12 
    cout << value3 << endl;
    return 0;
}

测试代码的运行结果：
运行结果

cout输出位数控制———整体输出位数的控制

通过setw(n)方法设置下一个输出量时，设定输出的长宽为n个字符。输出量不达n个字符时，会在输出量左边填补对应的空白；若宽于n个字符，则按实际需要全部输出：

1
2
3
4
5
6
7
8
9
10
11
 #include<iostream>
 #include<iomanip>
using namespace std;
int n;
int main() {
    while (cin >> n) {
        if (n == -1) break;
        cout << setw(5)<<n << endl;
    }
    return 0;
}

运行结果示意：
运行结果示意

cout靠左或者靠右输出的设置

1
2
3
4
5
6
//默认是右对齐.
cout <<left ;                                 // 左对齐
cout <<setw(5) <<12 <<setw(5) <<34 <<endl ;   // 12___34___

cout <<right ;                                // 默认 右对齐
cout <<setw(5) <<12 <<setw(5) <<34 <<endl ;   // ___12___34

物理相关计算与证明

    这里主要证明当认为卡牌长度为单位1，每次增加一张卡牌时，最底端的卡牌总是多于桌檐儿的长度为：L(i)=$\frac{1}{2 * i }$

力矩

    力矩 (moment of force) 力对物体产生转动作用的物理量。力对轴的矩是力对物体产生绕某一轴转动作用的物理量，其大小等于力在垂直于该轴的平面上的分量和此分力作用线到该轴垂直距离的乘积。

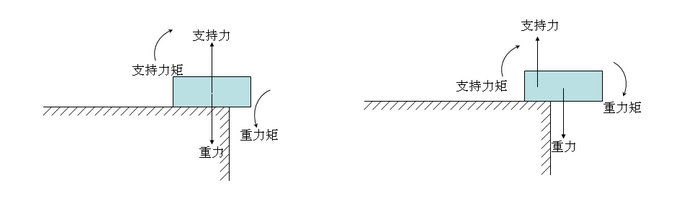
非临界情况

杠杆原理

    杠杆又分称费力杠杆、省力杠杆和等臂杠杆，杠杆原理也称为“杠杆平衡条件”。要使杠杆平衡，作用在杠杆上的两个力矩（力与力臂的乘积）大小必须相等。即：

动力×动力臂=阻力×阻力臂
用代数式表示为
F1·L1=F2·L2
    式中，F1表示动力，L1表示动力臂，F2表示阻力，L2表示阻力臂。从上式可看出，要使杠杆达到平衡，动力臂是阻力臂的几倍，阻力就是动力的几倍。

平衡条件时的计算证明

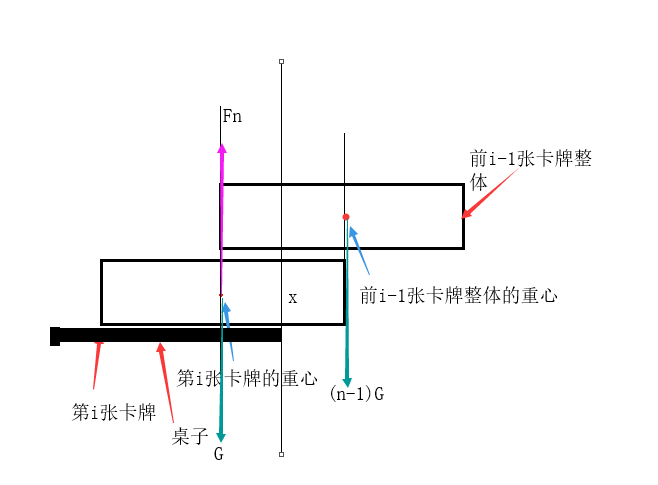
平衡时受力图

    对于i张卡片的最佳摆法，我们只需要在i-1张卡片的摆法下面加一张边缘与桌檐重合的卡片，并将所有卡片一起向桌檐外移动。
    对于一种最佳摆法，其中心一定在桌檐上，所以一定符合杠杆原理，支点是桌檐。
    那么对于i张卡片的情况，我们假设第n张向外移动了x，那么前n-1张的重心就在桌檐外x，因为他们的重心在i-1张卡片时原本在桌檐上。
第i张卡片的重心在桌檐内0.5-x处(规则的矩形重心在几何中心)，那么我们可以列出杠杆平衡方程：

(0.5-x)* G=x* (i-1)G

解得：x=$\frac{1}{2 * i }$

所以：
        第一张为 $\frac{1}{2}$
        第二张为 $\frac{1}{2}$+$\frac{1}{4}$
        第三张为 $\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$
        ……………………

Accepted代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include<iostream>
#include<iomanip>
using namespace std;
const int maxn = 99999 + 1;
double res[maxn];
int flag,n;
int main() {
    flag = 1;
    res[0] = 0;
    for (int i = 1; i < maxn; i++) res[i] += (res[i - 1] + 1.0 / ((double)i * 2.0));
    while (cin >> n) {
        if (n >= maxn)break;
        if (flag) {
            cout << "# Cards  Overhang" << endl;
            flag = 0;
        }
        
        cout << setw(5) << n << "     " << fixed << setprecision(3) << res[n] <<endl;
    }
    return 0;
}

参考博客

博主 金海峰的博客 的poj1607
博主 谙忆 的HDOJ 1330 Deck(叠木块-物理题啊！贪心算法用到了一点)

Author: Zoey

Link: https://zoey1038569979.github.io/2019/08/20/hdoj1330/

Copyright: All articles in this blog are licensed under CC BY-NC-SA 3.0 unless stating additionally.

< PreviousPost
校内算法考试（第三次）总结NextPost >
关于HDOJ 1326题(Box of Bricks) 的理解(C/C++)
CATALOG
  1. 1. Deck(桌檐叠卡牌)
  2. 2. 原题链接
  3. 3. cout输出控制（复习）
    1. 3.1. 小数位数的控制
    2. 3.2. cout输出位数控制———整体输出位数的控制
    3. 3.3. cout靠左或者靠右输出的设置
  4. 4. 物理相关计算与证明
    1. 4.1. 力矩
    2. 4.2. 杠杆原理
    3. 4.3. 平衡条件时的计算证明
  5. 5. Accepted代码
  6. 6. 参考博客