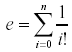关于HDOJ 1012题的理解(C/C++)

看起来蛮简单的一个题，但是还是没有能一次A的过，并且有学到如何在c++中控制输出的小数位数，于是感觉可以写到自己的博客里来。题意是很简单的，就让输出一下n取0-9的时候，对应的e用所给的公式计算出来的结果是多少。难点（大佬请别在意）的话，可能就是控制输出位数了。

题目描述

u Calculate e
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 59129 Accepted Submission(s): 27115

Problem Description
A simple mathematical formula for e is

where n is allowed to go to infinity. This can actually yield very accurate approximations of e using relatively small values of n.

Output
Output the approximations of e generated by the above formula for the values of n from 0 to 9. The beginning of your output should appear similar to that shown below.

Sample Output
n e

---

0 1
1 2
2 2.5
3 2.666666667
4 2.708333333

Source
Greater New York 2000

Recommend
JGShining

原题链接

More info:Question

小数位数的控制

首先是头文件

#include <iomanip>

然后就是用法了

cout << fixed<< setprecision(n)<< 变量;

当然，通过这次的题目还发现了一写小细节问题，之前都没怎么注意的。原来cout输出时，默认地，会删除掉多余的小数点后的0。于是去搜了一下怎么让cout输出不去删掉小数点后多余的0：

cout.setf(ios_base::fixed,ios_base::floatfield);

然后以下是自己结合网上给的关于控制小数位数的一些测试代码：

#include<iostream>
#include <iomanip>
using namespace std;
int main()
{
    const double value = 12.3456789;
    cout << value << endl; // 默认以6精度，所以输出为 12.3457 
    cout << setprecision(4) << value << endl; // 改成4精度，所以输出为12.35 
    cout << setprecision(8) << value << endl; // 改成8精度，所以输出为12.345679 
    cout << fixed << setprecision(4) << value << endl; // 加了fixed意味着是固定点方式显示，所以这里的精度指的是小数位，输出为12.3457 
    cout << value << endl; // fixed和setprecision的作用还在，依然显示12.3457 
    cout.unsetf(ios::fixed); // 去掉了fixed，所以精度恢复成整个数值的有效位数，显示为12.35 
    cout << value << endl;
    cout.precision(6); // 恢复成原来的样子，输出为12.3457 
    cout << value << endl<<endl;

    //在C++中，cout语句会自动删除浮点数小数部分多余的0
    const double value2 = 12.0000000;
    cout << value2 << endl; // 默认以6精度，但是cout语句会自动删除浮点数小数部分多余的0，所以输出为12
    cout << setprecision(4) << value2 << endl; // 改成4精度，输出为12 
    cout << setprecision(8) << value2<< endl; // 改成8精度，输出为12 
    cout << fixed << setprecision(4) << value2 << endl; // 加了fixed意味着是固定点方式显示，所以这里的精度指的是小数位，输出为12.0000 
    cout << value2 << endl; // fixed和setprecision的作用还在，依然显示12.0000 
    cout.unsetf(ios::fixed); // 去掉了fixed，精度恢复成整个数值的有效位数，但是依旧自动删除多余0，显示为12 
    cout << value2 << endl;
    cout.precision(6); // 恢复成原来的样子，输出为12 
    cout << value2 << endl<<endl;
    
    //cout.setf(ios_base::fixed,ios_base::floatfield);可避免自动删除多余0的效果
    const double value3 = 12.0000000;
    cout.setf(ios_base::fixed, ios_base::floatfield);
    cout << value3 << endl; // 默认以6精度，所以输出为 12.000000 
    cout << setprecision(4) << value3 << endl; // 改成4精度，所以输出为12.0000 
    cout << setprecision(8) << value3 << endl; // 改成8精度，所以输出为12.00000000 
    cout << fixed << setprecision(4) << value3 << endl; // 加了fixed意味着是固定点方式显示，所以这里的精度指的是小数位，输出为12.0000 
    cout << value3 << endl; // fixed和setprecision的作用还在，依然显示12.0000 
    cout.unsetf(ios::fixed); // 去掉了fixed，所以精度恢复成整个数值的有效位数，显示为12 
    cout << value3 << endl;
    cout.precision(6); // 恢复成原来的样子，输出为12 
    cout << value3 << endl;
    return 0;
}

测试代码的运行结果：

Accepted代码

#include<iostream>
#include <iomanip>
using namespace std;
double ans[11],res;
int main() {
    ans[0] = 1.0;
    for (int i = 1; i <= 9; i++) {
        ans[i] = ans[i - 1] * (1.0 / i);
    }
    
    cout << "n e" << endl;
    cout << "- -----------" << endl;
    for (int i = 0; i <= 9; i++) {
        res = 0.0;
        for (int j = 0; j <= i; j++) {
            res += ans[j];
        }
        if (i == 0) {
            cout << "0 1\n";
            cout << "1 2\n";
            cout << "2 2.5\n";
        }
        if(i>=3) cout << i << " " <<fixed<< setprecision(9)<< res << endl;
    }
    return 0;
}

这里提醒下，由于自己没注意，原本很简单的题都提交了好几遍才过。主要在前三个输出，由于之后是控制了位数为9为小数位的，所以前三个根据样例输出的提示，应该是不需要多余小数点后的0的。所以简单粗暴地直接给他手动打出来了，23333333333。